Древнеегипетская десятичная непозиционная система
В древнеегипетской системе счисления, которая возникла во второй половине третьего тысячелетия до н.э., использовались специальные цифры для обозначения чисел 1, 0, 102,103, 104, 105, 10 6, 10 7. Числа в египетской системе счисления записывались как комбинации этих цифр, в которых каждая из них повторялась не более девяти раз.
Число 345 древние египтяне записывали так:
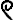
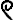
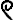
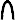
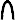
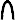
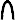
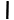
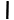
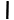
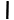
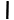 ,
,
где
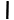 — единицы,
— единицы,
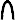 — десятки,
— десятки,
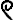 — сотни,
— сотни,
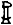 — тысячи.
— тысячи.
В основе древнеегипетской системы счисления лежал простой принцип сложения, согласно которому значение числа равно сумме значений цифр, участвующих в его записи. Ученые относят древнеегипетскую систему счисления к десятичной непозиционной.
Числовая система индейцев Майя
"В письменности майа, как и в других иероглифических системах письма, употребляются знаки фонетические (алфавитные и слоговые), идеографические (обозначающие целые слова) и ключевые (поясняющие значения слов, но не читающиеся). Один и тот же знак в разных сочетаниях может употребляться то как фонетический, то как ключевой, то как идеограмма..."Юрий Кнорозов
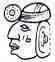
Иероглифические символы чисел майя от 1 до 10.

|

|
|

|

|

|

|

|

|

|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Вавилонская шестидесятеричная система
Также далеко от наших дней, за две тысячи лет до н.э., в другой великой цивилизации — вавилонской — люди записывали цифры по-другому.
Числа в этой системе счисления составлялись из знаков двух видов: прямой клин
 служил для обозначения единиц, а лежачий клин —
служил для обозначения единиц, а лежачий клин —
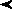 — для обозначения десятков. Число 32, например, записывали так:
— для обозначения десятков. Число 32, например, записывали так:
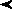
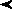
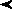

 . Знаки
. Знаки
 и
и
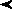 служили цифрами в этой системе. Число 60 снова обозначалось тем же знаком
служили цифрами в этой системе. Число 60 снова обозначалось тем же знаком
 , что и 1, этим же знаком обозначались и числа 3600=602, 216000=603 и все другие степени 60. Поэтому вавилонская система счисления получила название
шестидесятеричной.
, что и 1, этим же знаком обозначались и числа 3600=602, 216000=603 и все другие степени 60. Поэтому вавилонская система счисления получила название
шестидесятеричной.
Для определения значения числа надо было изображение числа разбить на разряды справа налево. Новый разряд начинался с появления прямого клина после лежачего, если рассматривать число справа налево.


|
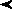


|
| 2-й разряд | 1-й разряд |
Значение числа определяли по значениям состовляющих его цифр, но с учетом того, что цифры в каждом последующем разряде значили в 60 раз больше тех же цифр в предыдущем разряде.
Число 92=60+32 записывали так:

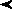
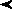
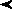

 , а число 444 в этой системе записи чисел имело вид
, а число 444 в этой системе записи чисел имело вид







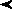
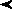



 , так как 444=7 · 60+24.
, так как 444=7 · 60+24.
Все числа от 1 до 59 вавилонян записывали в десятичной непозиционной системе, а число в целом — в позиционной системе с основанием 60.
Запись числа у вавилонян была неоднозначной, так как не существовало цыфры для обозначения нуля. Запись числа 92, приведенная выше, могла обозначать не только 92=60+32, но и, 3632=3600+32=602+32.
Для определения абсолютного значения числа требовались дополнительные сведения. Впоследствии вавилоняне ввели специальный символ для обозначения пропущенного
шестидесятеричного разряда —
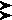 , что соответствует появлению цифры 0 в записи десятичного числа.
, что соответствует появлению цифры 0 в записи десятичного числа.
Число 3632 теперь нужно было записывать так:

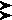
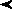
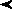
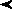

 . Но в конце числа этот символ все же не ставился, т.е. этот символ все же не был цифрой "ноль" в ношем понимании, и опять же требовались дополнительные
сведения для того, чтобы отличить 1 от 60, от 3600 и т.д.
. Но в конце числа этот символ все же не ставился, т.е. этот символ все же не был цифрой "ноль" в ношем понимании, и опять же требовались дополнительные
сведения для того, чтобы отличить 1 от 60, от 3600 и т.д.
Таблицу умножения вавилоняне никогда не запоминали, т.к. это было практически невозможно. При вычислениях использовались готовые таблицы умножения.
Шестидесятеричная вавилонская система — первая известная нам система счисления, частично основанная на позиционном принципе.
Мнения историков по поводу того, как именно возникла эта система счисленя, расходятся. Существуют две гипотезы. Первая исходит из того, что произошло слияние двух племён, одно из которых пользовалось шестеричной, другое — десятичной.
Шестидесятиричная система счисления в данном случае могла возникнуть в результате своеобразного политического компромисса. Суть второй гипотезы в том, что древние вавилоняне считали продолжительность года равной 360 суткам, что естественно связано с числом 60. Отголоски использования этой системы счисления дошли до наших дней. Например, 1 час = 60 минутам, 1 градус = 60 минутам. В целом шестидесятиричная система счисления громоздка и неудобна.
Система вавилонян сыграла большую роль в развитии матаматики и астрономии, ее следы сохранились и до наших дней. Так, мы до сих пор делим час на 60 минут, а минуты на 60 секунд. Следуя примеру вавилонян, мы и окружность делим на 360 частей (градусов).
Римская система
Знакомая нам римская система не слишком принципиально отличается от египетской. В ней для обозначения чисел 1, 5, 10, 50, 100, 500 и 1000 используются заглавные латинские буквы I, V, X, L, C, D и M соответственно, являющиеся цифрами этой системы счисления.
| I | V | X | L | C | D | M |
| 1 | 5 | 10 | 50 | 100 | 500 | 1000 |
Число в римской системе счисления обозначается набором стоящих подряд цифр. Значение числа равно:
1) сумме значений идущих подряд нескольких одинаковых цифр (назовем их группой первого вида);
2) разности значений двух цифр, если слева от большей цифры стоит меньшая. В этом случае от значения большей цифры отнимается значение меньшей цифры. Вместе они образуют группу второго вида. Заметим, что левая цифра может быть меньше правой максимум на один порядок: так, перед L (50) и C (100) из "младших" может стоять только X (10), перед D (500) и M(1000) — только C (100), перед V (5) — только I (1);
3) сумме значений групп и цифр, не вошедших в группы первого или второго вида.
Например, IX обозначает 9, XI обозначает11. Десятичное число 28 представляется следующим оброзом: XXVIII=10+10+5+1+1+1, а десятичное число 99 имеет вот такое представление: IC= -1+100.
Число 32 в римской системе счисления имеет вид XXXII=(X+X+X)+(I+I)=30+2 (две группы первого вида).
Число 444, имеющее в своей десятичной записи 3 одинаковые цифры, в римской системе счисления будет записано в виде CDXLIV=(D-C)+(L-X)+(V-I)=400+40+4 (три группы второго вида).
Число 1974 в римской системе счисления будет иметь вид MCMLXXIV=M+(M-C)+L+(X+X)+(V-I)=1000+900+50+20+4 (наряду с группами обоих видов в формировании числа участвуют отдельные "цифры"). Вы видели подобные обозначения года выпуска в титрах голливудских фильмов.
Римская система счисления сегодня используется в основном для обозночения знаменательных и юбилейных дат, разделов и глав в книгах.
Двенадцатеричная система счисления
Довольно широкое распространение имела двенадцатеричная система счисления.
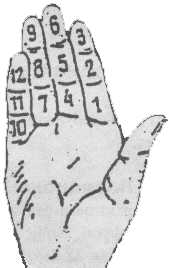 Происхождение её тоже связано со счетом на пальцах. Считали большим
палецем руки фаланги остальных четырёх пальцев: всего их 12. Элементы
двенадцатеричной системы счисления сохранились в Англии в системе
мер (1 фут = 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам).
Нередко и мы сталкиваемся в быту с двенадцатеричной системой счисления:
чайные и столовые сервизы на 12 персон, комплект носовых платков
— 12 штук.
Происхождение её тоже связано со счетом на пальцах. Считали большим
палецем руки фаланги остальных четырёх пальцев: всего их 12. Элементы
двенадцатеричной системы счисления сохранились в Англии в системе
мер (1 фут = 12 дюймам) и в денежной системе (1 шиллинг = 12 пенсам).
Нередко и мы сталкиваемся в быту с двенадцатеричной системой счисления:
чайные и столовые сервизы на 12 персон, комплект носовых платков
— 12 штук.
Числа в английском языке от одного до двенадцати имеют свое название, последующие числа являются составными.
| 1 -- one | 2 -- two | 3 -- three | 4 -- four | 5 -- five | 6 -- six |
| 7 -- seven | 8 -- eight | 9 -- nine | 10 -- ten | 11 -- eleven | 12 -- twelve |
Алфавитные ситемы счисления
Алфавитные системы счисления представляют особую группу. В них для записи чисел использовался буквенный алфавит. Примером алфавитной системы счисления является славянская. У одних славянских народов числовые значения букв устанавливались в порядке следования букв славянского алфавита, у других, в частности у русских, роль цифр играли не все буквы, а только те, которые имеются в греческом алфавите.
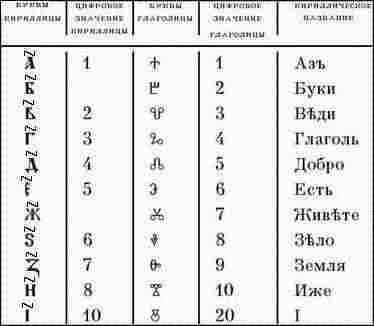
Над буквой, обозначающей цифру, ставился специальный знак -- "титло" (отсюда - число). Славянская система счисления сохранилась в богослужебных книгах.
Алфавитная система счисления была распространена у древних армян , грузин, греков (ионическая система счисления), арабов, евреев и других народов Ближнего Востока.

